The hardware design of a digital audio recorder embodies fundamental principles such as sampling and quantizing.
The analog signal is sampled and quantized and converted to numerical form prior to storage, transmission, or processing. Subsystems such as dither generator, anti aliasing filter, sample-and-hold, analog-to-digital converter, and channel code modulator constitute the hardware encoding chain. Although other architectures have been devised, the linear pulse-code modulation (PCM) system is the most illustrative of the nature of audio digitization and is the antecedent of other methods. This Section and the next, focus on the PCM hardware architecture. Such a system accomplishes the essential pre- and postprocessing for either a digital audio recorder or a real-time digital processor.
The bandwidth of a recording or transmission medium measures the range of frequencies it’s able to accommodate with an acceptable amplitude loss. An audio signal sampled at a frequency of 48 kHz and quantized with 16-bit words comprises 48 kHz × 16 bits, or 768 kbps (thousand bits per second). With overhead for data such as synchronization, error correction, and modulation, the channel bit rate might be 1 Mbps (million bits per second) for a monaural audio channel. Clearly, unless bit-rate reduction is applied, considerable throughput capacity is needed for digital audio recording and transmission. It’s the task of the digital recording stage to encode the audio signal with sufficient fidelity, while maintaining an acceptable bit rate.
Pulse-Code Modulation
Modulation is a means of encoding information for purposes such as transmission or storage. In theory, many different modulation techniques could be used to digitally encode audio signals. These techniques are fundamentally identical in their task of representing analog signals as digital data, but in practice they differ widely in relative efficiency and performance. Techniques such as amplitude modulation (AM) and frequency modulation (FM) have long been used to modulate carrier frequencies with analog audio information for radio broadcast. Because these are continuous kinds of modulation, they are referred to as wave-parameter modulation.
When conveying sampled information, various types of pulse modulation present themselves. For example, a pulse width or pulse position in time might represent the signal amplitude at sample time; pulse-width modulation (PWM) is an example of the former, and pulse-position modulation (PPM) is an example of the latter. In both cases, the original signal amplitude is coded and conveyed through constant amplitude pulses. A signal's amplitude can also be conveyed directly by pulses; pulse-amplitude modulation (PAM) is an example of this approach. The amplitude of the pulses equals the amplitude of the signal at sample time.
PWM, PPM, and PAM are shown in Fgrs. 1A through D.
In other cases, sample amplitudes are conveyed through numerical methods. For example, in pulse-number modulation (PNM), the modulator generates a string of pulses; the pulse count represents the amplitude of the signal at sample time; this is shown in Fgr. 1F. However , for high resolution, a large number of pulses are required.
Although PWM, PPM, PAM, and PNM are often used in the context of conversion, they are not suitable for transmission or recording because of error or bandwidth limitations.
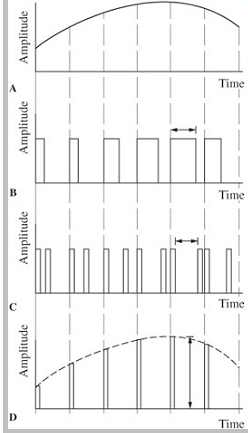
FGR. 1 PWM, PPM, and PAM are examples of pulse parameter modulation. PNM
and PCM are examples of numerical pulse parameter modulation. A. Analog waveform.
B. Pulse-width modulation. C. Pulse-position modulation. D. Pulse-amplitude
modulation. E. Quantized analog waveform. F. Pulse-number modulation. G. Pulse
code modulation.
The most commonly used modulation method is pulse code modulation (PCM). PCM was devised in 1937 by Alec Reeves while he was working as an engineer at the International Telephone and Telegraph Company laboratories in France. (Reeves also invented PWM.) In PCM, the input signal undergoes sampling, quantization, and coding. By representing the measured analog amplitude of samples with a pulse code, binary numbers can be used to represent amplitude. At the receiver, the pulse code is used to reconstruct an analog waveform. The binary words that represent sample amplitudes are directly coded into PCM waveforms as shown in Fgr. 1G.
With methods such as PWM, PPM, and PAM, only one pulse is needed to represent the amplitude value, but in PCM several pulses per sample are required. As a result, PCM might require a channel with higher bandwidth.
However, PCM forms a very robust signal in that only the presence or absence of a pulse is necessary to read the signal. In addition, a PCM signal can be regenerated without loss. Therefore the quality of a PCM transmission depends on the quality of the sampling and quantizing processes, not the quality of the channel itself. In addition, depending on the sampling frequency and capacity of the channel, several PCM signals can be combined and simultaneously conveyed with time-division multiplexing.
This expedites the use of PCM; for example, stereo audio is easily conveyed. Although other techniques presently exist and newer ones will be devised, they will measure their success against that of pulse-code modulation digitization. In most cases, highly specialized channel codes are used to modulate the signal prior to storage.
These channel modulation codes are also described in this Section.
The architecture of a linear PCM (sometimes called LPCM) system closely follows a readily conceptualized means of designing a digitization system. The analog waveform is filtered and time sampled and its amplitude is quantized with an analog-to-digital (A/D) converter. Binary numbers are represented as a series of modulated code pulses representing waveform amplitudes at sample times.
If two channels are sampled, the data can be multiplexed to form one data stream. Data can be manipulated to provide synchronization and error correction, and auxiliary data can be added as well. Upon playback, the data is demodulated, decoded, and error-corrected to recover the original amplitudes at sample times, and the analog waveform is reconstructed with a digital-to-analog (D/A) converter and lowpass filter.
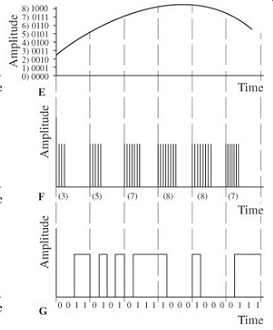
The encoding section of a conventional stereo PCM recorder consists of input amplifiers, a dither generator, input lowpass filters, sample-and-hold circuits, analog-to digital converters, a multiplexer, digital processing and modulation circuits, and a storage medium such as an optical disc or a hard-disk drive. An encoding section block diagram is shown in Fgr. 2. This hardware design is a practical realization of the sampling theorem. In practice, other techniques such as oversampling may be employed.
An audio digitization system is really nothing more than a transducer, which processes the audio signal for digital storage or transmission, then processes it again for reproduction. Although that sounds simple, the hardware must be carefully engineered; the quality of the reproduced audio depends entirely on the system's design. Each subsystem must be carefully considered.
FGR. 2 A linear PCM record section showing principal elements.
Dither Generator
Dither is a noise signal added to the input audio signal to remove quantization artifacts. As described in Section 2, dither causes the audio signal to vary between adjacent quantization levels. This action decorrelates the quantization error from the signal, removes the effects of the error, and encodes signal amplitudes below the amplitude of a quantization increment. However, although it reduces distortion, dither adds noise to the audio signal.
Perceptually, dither is beneficial because noise is more readily tolerated by the ear than distortion.
Analog dither, applied prior to A/D conversion, causes the A/D converter to make additional level transitions that preserve low-level signals through duty cycle, or pulse-width modulation. This linearizes the quantization process.
Harmonic distortion products , for example, are converted to wideband noise. Several types of dither signals, such as Gaussian, rectangular, and triangular probability density functions can be selected by the designer; in some systems, the user is free to choose a dither signal. The amplitude of the applied dither is also critical. In some cases, the input signal might have a high level of residual noise. For example, an analog preamplifier might have a noise floor sufficient to dither the quantizer. However, the digital system must provide a dynamic range that sufficiently captures all the analog information, including the signal within the analog noise floor, and must not introduce quantization distortion into it. The word length of the quantizer must be sufficient for the audio program, and its least significant bit (LSB) must be appropriately dithered. In addition, whenever the word length is reduced , for example, when a 20-bit master recording is transferred to the 16-bit format, dither must be applied, as well as noise shaping.
Dither is discussed more fully in Section 2; psychoacoustically optimized noise shaping is described in Section 18.
Input Lowpass Filter
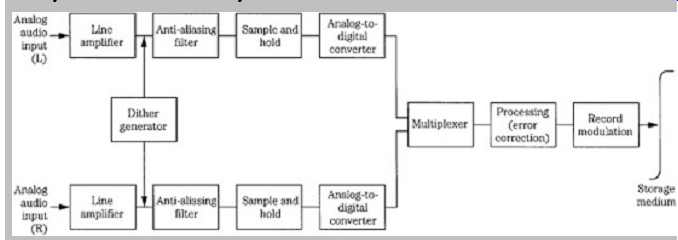
An input audio signal might have high-frequency content that is above the Nyquist (half-sampling) frequency. To ensure that the Nyquist theorem is observed, and thus prevent aliasing, digital audio systems must bandlimit the audio input signal, eliminating high-frequency content above the Nyquist frequency. This can be accomplished with an input lowpass filter, sometimes called an anti aliasing filter. In a system with a sampling frequency of 48 kHz, the ideal filter cutoff frequency would be 24 kHz. The input lowpass filter must attenuate all signals above the half-sampling frequency, yet not affect the lower in-band signals. Thus, an ideal filter is one with a flat passband, an immediate or brick-wall filter characteristic, and an infinitely attenuated stopband, as shown in Fgr. 3A. In addition to these frequency-response criteria, an ideal filter must not affect the phase linearity of the signal.
Although in practice an ideal filter can be approximated, its realization presents a number of engineering challenges. The filter's passband must have a flat frequency response; in practice some frequency irregularity (ripple) exists, but can be minimized. The stopband attenuation must equal or exceed the system's dynamic range, as determined by the word length. For example, a 16-bit system would require stopband attenuation of over -95 dB; a stopband attenuation of -80 dB would yield 0.01% alias distortion under worst-case conditions. Modern A/D converters use digital filtering and oversampling methods to perform anti-aliasing; this is summarized later in this Section, and described in detail in Section 18. Early systems used only analog input lowpass filters. Because they clearly illustrate the function of anti-aliasing filtering, and because even modern converters still employ low-order analog filters, analog lowpass filters are described below.

FGR. 3 Lowpass filter characteristics. A. An ideal lowpass filter has a flat
passband response and instantaneous cutoff. B. In practice, filters exhibit
ripple in the stopband and passband, and sloping cutoff.
In early systems (as opposed to modern systems that use digital filters) the input signal is lowpass filtered by an analog filter with a very sharp cutoff to bandlimit the signal to frequencies at or below the half-sampling frequency. A brick-wall cutoff demands compromise on specifications such as flat passband and low phase distortion. To alleviate the problems such as phase nonlinearities created by a brick-wall response, analog filters can use a more gradual cutoff. However, a low-order filter with a cutoff at the half-sampling frequency would roll off audio frequencies, hence its passband must be extended to a higher frequency. To avoid aliasing, the sampling frequency must be extended to ensure that the filter provides sufficient attenuation at the half-sampling frequency. A higher sampling frequency, perhaps three times higher than required for a brick-wall filter, might be needed; however, this would raise data bandwidth requirements. To limit the sampling frequency and make full use of the passband below the half-sampling point, a brick-wall filter is mandated. When a sampling frequency of 48 kHz is used, the analog input filters are designed for a flat response from dc to 22 kHz. This arrangement provides a guard band of 2 kHz to ensure that attenuation is sufficient at the half-sampling point. A practical lowpass filter characteristic is shown in Fgr. 3B.
Several important analog filter criteria are overshoot, ringing, and phase linearity. Sharp cutoff filters exhibit resonance near the cutoff frequency and this ringing can cause irregularity in the frequency response. The sharper the cutoff, the greater the propensity to ringing. Certain filter types have inherently reduced ringing. Phase response is also a factor. Lowpass filters exhibit a frequency dependent delay, called group delay, near the cutoff frequency, causing phase distortion. This can be corrected with an analog circuit preceding or following the filter, which introduces compensating delay to achieve overall phase linearity; this can yield a pure delay, which is inaudible. In the cases of ringing and group delay, there is debate on the threshold of audibility of such effects; it’s unclear how perceptive the ear is to such high-frequency phenomena.
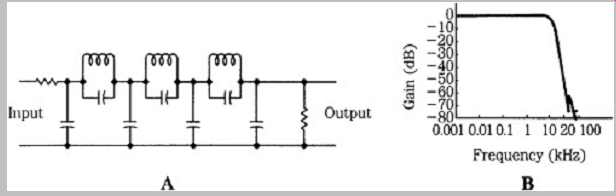
FGR. 4 An example of a Chebyshev lowpass filter and its frequency response.
A. A passive lowpass filter schematic. B. Lowpass filter frequency response
showing a steep cutoff.
Analog filters can be classified according to the mathematical polynomials that describe their characteristics. There are many filter types; For example, Bessel, Butter-worth, and Chebyshev filters are often used.
For each of these filter types, a basic design stage can be repeated or cascaded to increase the filter's order and to sharpen the cutoff slope. Thus, higher-order filters more closely approximate a brick-wall frequency response. For example, a passive Chebyshev lowpass filter is shown in Fgr. 4; its cutoff slope becomes steeper when the filter's order is increased through cascading. However, phase shift also increases as the filter order is increased. The simplest lowpass filter is a cascade of RC (resistor capacitor) sections; each added section increases the roll off slope by 6 dB/octave. Although the filter won’t suffer from overshoot and ringing, the passband will exhibit frequency response anomalies.
Resonant peaks can be positioned just below the cutoff frequency to smooth the passband response of a filter but not affect the roll-off slope; a Butterworth design accomplishes this. However, a high-order filter is required to obtain a sharp cutoff and deep stopband. For example, a design with a transition band 40% of an octave wide and a stopband of -80 dB would require a 33rd-order Butterworth filter.
A filter with a narrow transition band can be designed at the expense of passband frequency response. This can be achieved by placing the resonant peaks somewhat higher than in a Butterworth design. This is the aim of a Chebyshev filter. A 9th-order Chebyshev filter can achieve a ±0.1-dB passband ripple to 20 kHz, and stopband attenuation of -70 dB at 25 kHz.
One characteristic of most filter types is that attenuation continues past the necessary depth for frequencies beyond the half-sampling frequency. If the attenuation curve is flattened, the transition band can be reduced. Anti-resonant notches in the stopband are often used to perform this function. In addition, reactive elements can be shared in the design, providing resonant peaks and anti-resonant notches. This reduces circuit complexity. The result is called an elliptical, or Cauer filter. An elliptical filter has the steepest cutoff for a given order of realization. For example, a 7th-order elliptical filter can provide a ±0.25-dB passband ripple, 40% octave transition band, and a -80- dB stopband. In practice, a 13-pole design might be required.
In general , for a given analog filter order, Chebyshev and elliptical lowpass filters give a closer approximation to the ideal than Bessel or Butterworth filters, but Chebyshev filters can yield ripple in the passband and elliptical filters can produce severe phase nonlinearities. Bessel filters can approximate a pure delay and provide excellent phase response; however, a higher-order filter is needed to provide a very high rate of attenuation. Butterworth filters are usually flat in the passband, but can exhibit slow transient response. No analog filter is ideal, and there is a trade-off between a high rate of attenuation and an acceptable time-domain response.
In practice, as noted, because of the degradation introduced by analog brick-wall filters, all-analog designs have been superseded by A/D converters that employ a low-order analog filter, oversampling, and digital filtering as discussed later in this Section and described in detail in Section18. Whatever method is used, an input filter is required to prevent aliasing of any frequency content higher than the Nyquist frequency.
Sample-and-Hold Circuit
As its name implies, a sample-and-hold (S/H) circuit performs two simple yet critical operations. It time-samples the analog waveform at a periodic rate, putting the sampling theorem into practice. It also holds the analog value of the sample while the A/D converter outputs the corresponding digital word. This is important because otherwise the analog value could change after the designated sample time, causing the A/D converter to output incorrect digital words. The input and output responses of an S/H circuit are shown in Fgr. 5. The output signal is an intermediate signal, a discrete PAM staircase representing the original analog signal, but is not a digital word. The circuit is relatively simple to design; however, it must accomplish both of its tasks accurately.
Samples must be captured at precisely the correct time and the held value must stay within tolerance. In practice, the S/H function is built into the A/D converter. The S/H circuit is also known as a track-hold circuit.
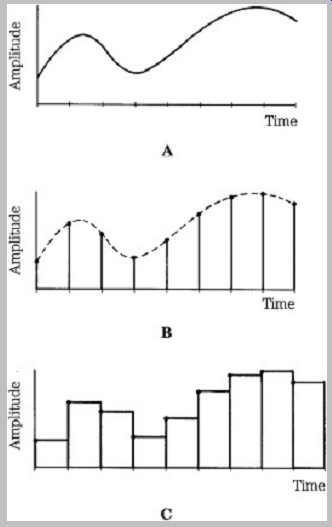
FGR. 5 The sample-and-hold circuit captures an analog value and holds it
while A/D conversion occurs. A. Analog input signal. B. Sampled input. C. Analog
held output.
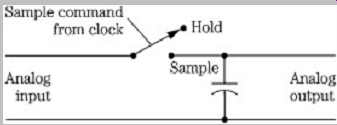
FGR. 6 A conceptual sample-and-hold circuit contains a switch and storage
element. The switch is closed to sample the signal.
As we have seen, time and amplitude information can completely characterize an acoustic waveform. The S/H circuit is responsible for capturing both informational aspects from the analog waveform. Samples are taken at a periodic rate and reproduced at the same periodic rate.
The S/H circuit accomplishes this time sampling. A clock, an oscillator circuit that outputs timing pulses, is set to the desired sampling frequency, and this command signal controls the S/H circuit.
Conceptually, an S/H circuit is a capacitor and a switch.
The circuit tracks the analog signal until the sample command causes the digital switch to isolate the capacitor from the signal; the capacitor holds this analog voltage during A/D conversion. A conceptual S/H circuit is shown in Fgr. 6. The S/H circuit must have a fast acquisition time that approaches zero; otherwise, the value output from the A/D converter will be based on an averaged input over the acquisition time, instead of the correct sample value at an instant in time. In addition, varying sample times result in acquisition timing error; to prevent this, the S/H circuit must be carefully designed and employ a sample command that is accurately clocked.
Jitter is any variation in absolute timing; in this case, variation in the sampling signal is shown in Fgr. 7. Jitter adds noise and distortion to the sampled signal, and must be limited in the clock used to switch the S/H circuit. Jitter is particularly significant in the case of a high-amplitude, high-frequency input signal. The timing precision required for accurate A/D conversion is considerable. Depending on the converter design , for example, jitter at the S/H circuit must be less than 200 ps (picosecond) to allow 16-bit accuracy from a full amplitude, 20-kHz sine wave, and less than 100 ps for 18-bit accuracy. Only then would the resulting noise components fall below the quantization noise floor. Clearly, S/H timing must be controlled by a clock designed with a highly accurate crystal quartz oscillator. Jitter is discussed in Section 4.
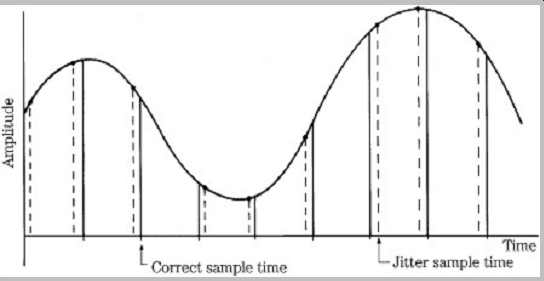
FGR. 7 Jitter is a variation in sample times that can add noise and distortion
to the output analog signal.
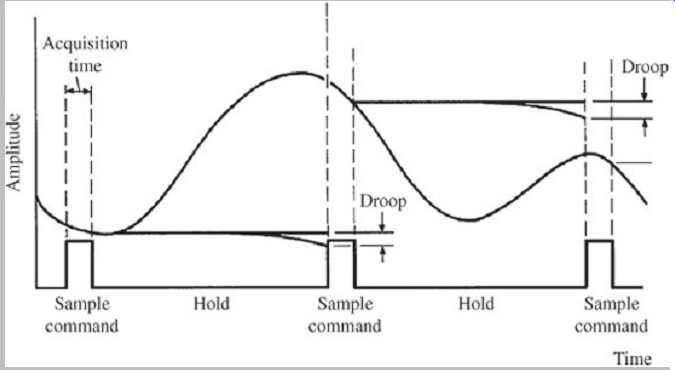
FGR. 8 Acquisition time and droop are two error conditions in the sample-and-hold
circuit.
Acquisition time is the time between the initiation of the sample command and the taking of the sample. This time lag can result in a sampled value different from the one present at the correct sample time. The effect of the delay is a function of the amplitude of the analog signal. It’s therefore important to minimize acquisition time. The S/H circuit's other primary function is to hold the captured analog voltage while conversion takes place. This voltage must remain constant because any variation greater than a quantization increment can result in an error at the A/D output. The held voltage can be prone to droop because of current leakage. Droop is the decrease in hold voltage as the storage capacitor leaks between sample times. Care in circuit design and selection of components can limit droop to less than one-half a quantization increment over a 20-µs period. For example, a 16-bit, ±10-V range A/D converter must hold a constant value to within 1 mV during conversion. Acquisition time error and droop are illustrated in Fgr. 8.
The demands of fast acquisition time and low droop are in conflict in the design of a practical S/H circuit. For fast acquisition time, a small capacitor value is better, permitting faster charging time. For droop, however, a large-valued capacitor is preferred, because it’s better able to retain the sample voltage at a constant level for a longer time. However, capacitor values of approximately 1 nF can satisfy both requirements. In addition, high-quality capacitors made of polypropylene or Teflon dielectrics can be specified. These materials can respond quickly, hold charge, and minimize dielectric absorption and hysteresis--phenomena that cause voltage variations.
In practice, an S/H circuit must contain more than a switch and a capacitor. Active circuits such as operational amplifiers must buffer the circuit to condition the input and output signals, speed switching time, and help prevent leakage. Only a few specialized operational amplifiers meet the required specifications of large bandwidth and fast settling time. Junction field-effect transistor (JFET) operational amplifiers usually perform best. Thus, a complete S/H circuit might have a JFET input operational amplifier to prevent source loading, improve switching time, isolate the capacitor, and supply capacitor-charging current. The S/H switch itself may be a JFET device, selected to operate cleanly and accurately with minimal jitter, and the capacitor may exhibit low hysteresis. A JFET operational amplifier is usually placed at the output to help preserve the capacitor's charge.
Analog-to-Digital Converter
The analog-to-digital (A/D) converter lies at the heart of the encoding side of a digital audio system, and is perhaps the single most critical component in the entire signal chain. Its counterpart, the digital-to-analog (D/A) converter, can subsequently be improved for higher fidelity playback.
However, errors introduced by the A/D converter will accompany the audio signal throughout digital processing and storage and, ultimately, back into its analog state. Thus the choice of the A/D converter irrevocably affects the fidelity of the resulting signal.
Essentially, the A/D converter must examine the sampled input signal, determine the quantization level nearest to the sample's value, and output the binary code that is assigned to that level-accomplishing those tasks in one sampling period (20 µs for a 48-kHz sampling frequency). The precision required is considerable: 15 parts per million for 16-bit resolution, 4 parts per million for 18-bit resolution, and 1 part per million for 20-bit resolution.
In a traditional A/D design, the input analog voltage is compared to a variable reference voltage within a feedback loop to determine the output digital word; this is known as successive approximation. More common oversampling A/D converters are summarized in this Section and discussed in detail in Section18.
The A/D converter must perform a complete conversion on each audio sample. Furthermore, the digital word it provides must be an accurate representation of the input voltage. In a 16-bit successive approximation converter, each of the 65,536 intervals must be evenly spaced throughout the amplitude range, so that even the least significant bit in the resulting word is meaningful. Thus, speed and accuracy are key requirements for an A/D converter. Of course, any A/D converter will have an error of ±1/2 LSB, an inherent limitation of the quantization process itself. Furthermore, dither must be applied.
The conversion time is the time required for an A/D converter to output a digital word; it must be less than one sampling period. Achieving accurate conversion from sample to sample is sometimes difficult because of settling time or propagation time errors. The result of accomplishing one conversion might influence the next. If a converter's input moves from voltage A to B and then later from C to B, the resulting digital output for B might be different because of the device's inability to properly settle in preparation for the next measurement. Obviously, dynamic errors grow more severe with demand for higher conversion speed. In practice, speeds required for low noise and distortion can be achieved. Indeed, many A/D converters simultaneously process two waveforms, alternating between left and right channels. Other converters can process 5.1 channels of input audio signals.
Numerous specifications have been devised to evaluate the performance accuracy of A/D converters. Amplitude linearity compares output versus input linearity. Ideally, the output value should always correspond exactly with input level, regardless of level. To perform the test, a series of tones of decreasing amplitude, or a fade-to-zero tone, is input to the converter. The tone is dithered with rectangular pdf dither. A plot of device gain versus input level will reveal any deviations from a theoretically flat (linear) response.
Integral linearity measures the "straightness" of the A/D converter output. It describes the transition voltage points, the analog input voltages at which the digital output changes from one code to the next, and specifies how close they are to a straight line drawn through them. In other words, integral linearity determines the deviation of an actual bit transition from the ideal transition value, at any level over the range of the converter. Integral linearity is illustrated in Fgr. 9A. Integral linearity is tested, and the reference line is drawn across the converter's full output range. Integral linearity is the most important A/D specification and is not adjustable. An n-bit converter is not a true n-bit converter unless it guarantees at least ±1/2 LSB integral linearity. The converter in Fgr. 9A has a ±1/4 LSB integral linearity.
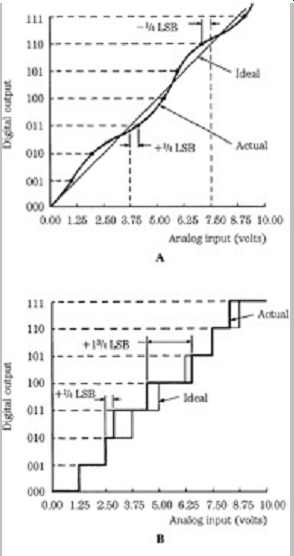
FGR. 9 Performance of an A/D converter can be specified in a variety of ways.
A. Integral linearity specification of an A/D converter. B. Differential linearity
specification of an A/D converter. C. Absolute accuracy specification of an
A/D converter.
Differential linearity error is the difference between the actual step height and the ideal value of 1 LSB. It can be measured as the distance between transition voltages, that is, the widths of individual input voltage steps. Differential linearity is shown in Fgr. 9B. Ideally, all the steps of an A/D transfer function should be 1 LSB wide. A maximum differential linearity error of ±1/2 LSB means that the input voltage might have to increase or decrease as little as 1/2 LSB or as much as 1 1/2 LSB before an output transition occurs. If this specification is exceeded, to perhaps ±1 LSB, some steps could be 2 LSBs wide and others could be 0 LSB wide; in other words, some output codes would not exist. High-quality A/D converters are assured of having no missing codes over a specified temperature range. The converter in Fgr. 9B has an error of ±1/2 LSB; some levels are 1/4 LSB wide, others are 1 1/2 LSB wide.
Conversion speed can affect both integral linearity and differential linearity errors. Quality A/D converters are guaranteed to be monotonic; that is, the output code either increases or remains the same for increasing analog input signals. If differential error is greater than 1 LSB, the converter will be nonmonotonic.
Absolute accuracy error, shown in Fgr. 9C, is the difference between the ideal level at which a digital transition occurs and where it actually occurs. A good A/D converter should have an error of less than ±1/2 LSB.
Offset error, gain error, or noise error can affect this specification. For the converter in Fgr. 9C, each interval is 1/8 LSB in error. In practice, otherwise good successive approximation A/D converters can sometimes drift with temperature variations and thus introduce inaccuracies.
Code width, sometimes called quantum, is the range of analog input values for which a given output code will occur.
The ideal code width is 1 LSB. A/D converters can exhibit an offset error as well as a gain error. An A/D converter connected for unipolar operation has an analog input range from 0 V to positive full scale. The first output code transition should occur at an analog input value of 1/2 LSB above 0 V. Unipolar offset error is the deviation of the actual transition value from the ideal value. When connected in a bipolar configuration, bipolar offset is set at the first transition value above the negative full-scale value.
Bipolar offset error is the deviation of the actual transition value from the ideal transition value at 1/2 LSB above the negative full-scale value. Gain error is the deviation of the actual analog value at the last transition point from the ideal value, where the last output code transition occurs for an analog input value 1 1/2 LSB below the nominal positive full-scale value. In some converters, gain and offset errors can be trimmed at the factory, and might be further zeroed with the use of external potentiometers. Multiturn potentiometers are recommended for minimum drift over temperature and time.
Harmonic distortion is a familiar way to characterize audio linearity and can be used to evaluate A/D converter performance. A single pure sine tone is input to the device under test, and the output is examined for spurious content other than the sine tone. In particular, spectral analysis will show any harmonic multiples of the input frequency. Total harmonic distortion (THD) is the ratio of the summed root mean square (rms) voltage of the harmonics to that of the input signal. To further account for noise in the output, the measurement is often called THD+N. The figure is usually expressed as a decibel figure or a percentage; however, visual examination of the displayed spectral output is a valuable diagnostic. It’s worth noting that in most analog systems, THD+N decreases as the signal level decreases.
The opposite is true in digital systems. Therefore, THD+N should be specified at both high and low signal levels.
THD+N should be evaluated versus amplitude and versus frequency, using FFT analysis.
Dynamic range can also be used to evaluate converter performance. Dynamic range is the amplitude range between a maximum-level signal and the noise floor. Using the EIAJ specification, dynamic range is typically measured by reading THD+N at an input amplitude of -60 dB; the negative value is inverted and added to 60 dB to obtain dynamic range. Also, signal-to-noise ratio (examining idle channel noise) can be measured by subtracting the idle noise from the full-scale signal. For consistency, a standard test sequence such as the ITU CCITT 0.33.00 (monaural) and CCITT 0.33.01 (stereo) can be used; these comprise a series of tones and are useful for measuring parameters such as frequency response, distortion, and signal to noise.
Noise modulation is another useful measurement. This test measures changes in the noise floor relative to changes in signal amplitude; ideally, there should be no correlation. In practice, because of low-level nonlinearity in the converter, there may be audible shifts in the level or tonality of the background noise that correspond to changes in the music signal. Precisely because the shifts are correlated to the music, they are potentially much more perceptible than benign unchanging noise. In one method used to observe noise modulation, a low-frequency sine tone is input to the converter; the sine tone is removed at the output and the spectrum of the output signal is examined in 1/3-octave bands. The level of the input signal is decreased in 5-dB steps and the test is repeated. Deviation in the noise floor by more than a decibel in any band across the series of tested amplitudes may indicate potentially audible noise modulation.
As noted, an A/D converter is susceptible to jitter, a variation in the timebase of the clocking signal. Random noise jitter can raise the noise floor and periodic jitter can create sidebands, thus raising distortion levels. Generally, the higher the specified dynamic range of the converter, the lower the jitter level. A simple way to test an A/D converter for jitter limitations is to input a 20-kHz, 0-dBFS (full amplitude) sine tone, and observe an FFT of the output signal. Repeat with a 100-Hz sine tone. An elevated noise floor at 20 kHz compared to 100 Hz indicates a potential problem from random-noise jitter, and discrete frequencies at 20 kHz indicate periodic jitter. High-quality A/D converters contain internal clocks that are extremely stable, or when accepting external clocks, have clock recovery circuitry to reject jitter disturbance. It’s incorrect to assume that one converter using a low-jitter clock will necessarily perform better than another converter using a high-jitter clock; actual performance depends very much on converter design. Even when jitter causes no data error, it can cause sonic degradation. Its effect must be carefully assessed in measurements and listening tests. Jitter is discussed in more detail in Section 4.
The maximum analog signal level input to an A/D converter should be scaled as close as possible to the maximum input conversion range, to utilize the converter's maximum signal resolution. Generally, a converter can be driven by a very low impedance source such as the output of a wideband, fast-settling operational amplifier.
Transitions in a successive approximation A/D converter's input current might be caused by changes in the output current of the internal D/A converter as it tests bits. The output voltage of the driving source must remain constant while supplying these fast current changes.
Changes in the dc power supply can affect an A/D converter's accuracy. Power supply deviations can cause changes in the positive full-scale value, resulting in a proportional change in all code transition values, that is, a gain error. Normally, regulated power supplies with 1% or less ripple are recommended. Power supplies should be bypassed with a capacitor--for example, 1 to 10 µF tantalum-located near the converter, to obtain noise-free operation. Noise and spikes from a switching power supply must be carefully filtered. To minimize jitter effects, accurate crystal clocks must be used to clock all A/D and S/H circuits.
Sixteen-bit resolution was formerly the quality benchmark for most digital audio devices, and it can yield excellent audio fidelity. However, many digital audio devices now process or store more than 16 bits. A digital signal processing (DSP) chip might internally process 56 bit words; this resolution is needed so that repetitive calculations won’t accumulate error that could degrade audio fidelity. In addition , for example, Blu-ray discs can store 20- or 24-bit words. Thus, many A/D and D/A converters claim conversion of up to 24 bits. However, it’s difficult or impossible to achieve true 24-bit conversion resolution with current technology. A resolution of 24 bits ostensibly yields a quantization error floor of about -145 dBFS (dB Full Scale). If a dBFS of 2 V rms is used, then a level at -145 dBFS corresponds to about 0.1 µV rms. This is approximately the level of thermal noise in a 6-ohm resistor at room temperature. The ambient noise in any practical signal chain would preclude ideal 24-bit resolution. Internal processing does require longer word lengths, but it’s unlikely that A/D or D/A converters will process signals at such high resolution.